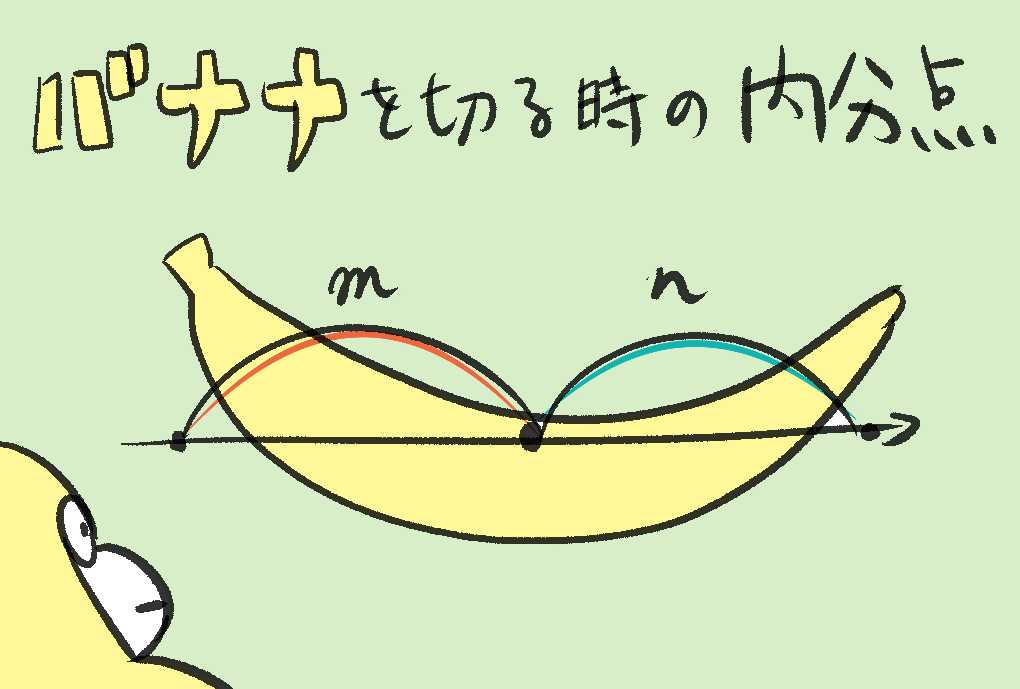
ゴリラと学ぶ「内分」

作成: 2020-03-18 | 更新: 2020-03-18

gori0000064

ついこの間、あるゴリラ🦍の兄弟がバナナ🍌をわけあうことをやったウホ。なかのいいきょうだいでほっこりしていることを思いだしたウホ。

あのときは、兄ゴリラが弟ゴリラにバナナを分けてあげていたウホ。このときには比例式の計算をして、具体的な長さを求めていたウホ。

ゴリはそのあと、ふと、比例式でわけるのはいいけど、じゃあその分けたちょうどの点はどうやってあらわせばいいか疑問に思ったウホ。

というわけで、こんかいはある線分を内分するときについて、その計算をやってみるウホ。

もんだい

あるゴリラのきょうだい🦍が、一本のバナナ🍌を分けることにしたウホ。
一本のバナナの長さは23.2 cmで、これをひとくちずつ分けていくことにしたウホ。

いま、兄ゴリラと弟ゴリラが、9.3 : 13.9でわけることにしたウホ。
このとき、内分する点の座標はどのようになるウホ？

🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍

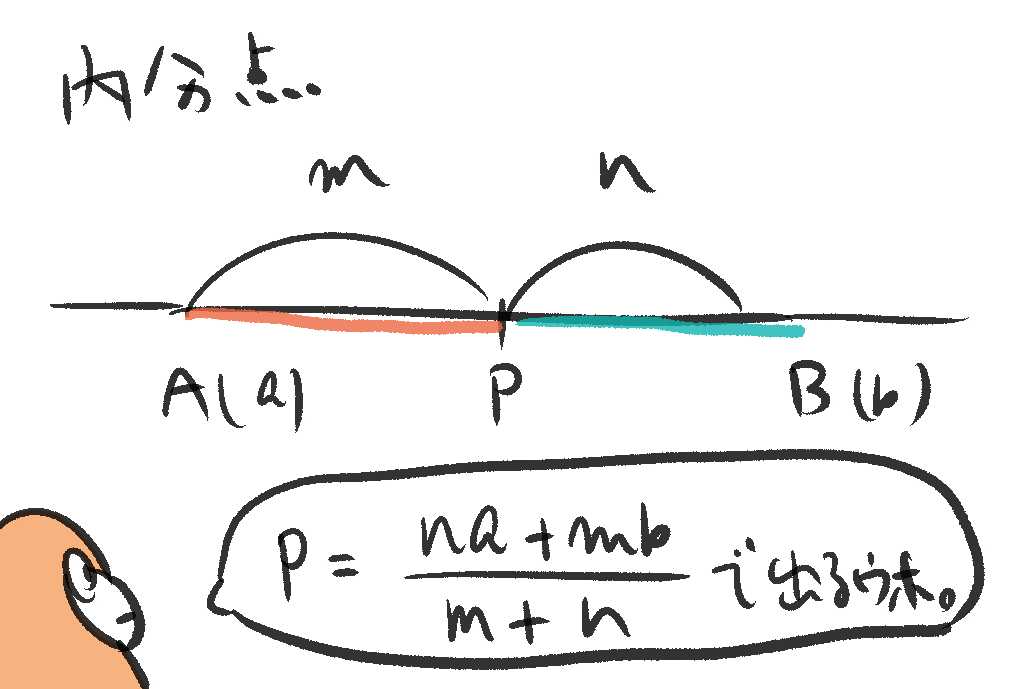
ニンゲンが高校でならう、内分の考え方を使うウホ。内分は、ある線分ABを点Pがm:nにわける、みたいなことを「m:nに内分する」という言い方をしていたウホ。

この計算方法は次のようになるウホ。証明してもいいけど、とりあえず公式をつかっちゃうウホ。

$内分点Pの座標は、\frac{na+mb}{m+n}$

これをつかって計算するウホ！さっくりと計算するために、二点A, Bをきめるウホ。
この2点ABは、23.2 cmのバナナについていうと、A(0)、B(23.2)としてしまっていいと思うウホ。
そうして計算をすると、

$\frac{13.9 × 0 + 9.3 × 23.2}{9.3 + 13.9} = 9.3$

になるウホ！そうすると、数直線が左に行くほど増加する場合、9.3 cmの点が内分点ということになるウホ。

gori0000064-2

座標の上で、どこが内分点なのかということを決めることができたウホ！

こたえ：内分点は9.3 cmのところ

こうして座標として点をきめておくことで、なんとなくこのあたりで切る、というなんとなくな感じから、きっちりと切るための点をつくることができたウホ！
もちろん、ふつうに手でちぎる分にはもんだいないけど、メカゴリラに切らせるときなんかは座標できめちゃった方が便利そうウホ！