ゴリラと学ぶ「比例式」

ゴリがジャングルを歩いていると、あるゴリラ🦍の兄弟がバナナ🍌をわけあおうとしているウホ。なかのいいきょうだいのようで、けんかすることなくおたがいにゆずり合っているウホ。とてもなかむつまじいウホ。

すると、兄ゴリラが弟ゴリラに、バナナをある割合でわけあうように提案したウホ。やさしい兄ゴリラは、弟ゴリラよりも少ない割合のバナナを手に入れることを提案しているウホ。でも、どうやら兄弟ゴリラにはけいさんのほうほうが分らないらしいウホ。

兄弟のやさしさに触れたゴリはつよく感銘をうけ、兄弟ゴリラの計算を手伝うことにしたウホ。

というわけで、こんかいは割合をつかった比例式についてといてみるウホ。

---

もんだい

あるゴリラのきょうだい🦍が、一本のバナナ🍌を分けることにしたウホ。
一本のバナナの長さは23.2 cmで、これをひとくちずつ分けていくことにしたウホ。

兄ゴリラは、弟ゴリラに多く食べさせてあげたいから、バナナの6割を弟にあげることにしたウホ。
このとき、兄ゴリラと弟ゴリラの食べるバナナは、それぞれ何 cmになるウホ？

🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍

---

こたえ

ニンゲンが中学校でならう、比例式の考え方を使うウホ。これは比の計算をすることで、目的の数を計算するほうほうウホ。

さっそくざっくりと計算していくと、いま、弟ゴリラはバナナの6割を食べることができるウホ。そうすると、兄ゴリラはのこりの割合、すなわち4割のバナナを食べることができるウホ。

割合だとけいさんしにくいから、小数に直すと、それぞれ0.6、0.4になるウホ。60%と40%とおなじ意味になるウホ。

で、これを比例式の形にするウホ。兄が食べられるバナナの長さを$x$とおくと、弟が食べられるバナナは全体（23.2 cm）から$x$ cmをひいた、$23.2 - x$ cmということになるウホ。このことから、つぎの比例式がつくれるウホ。

$x : 23.2 - x = 0.6 : 0.4$

で、ざっくりとした説明だけど、比例式のけいさんは内側どうしをかけたものと、外側どうしをかけたものをイコールで結ぶ、というものがあったウホ。

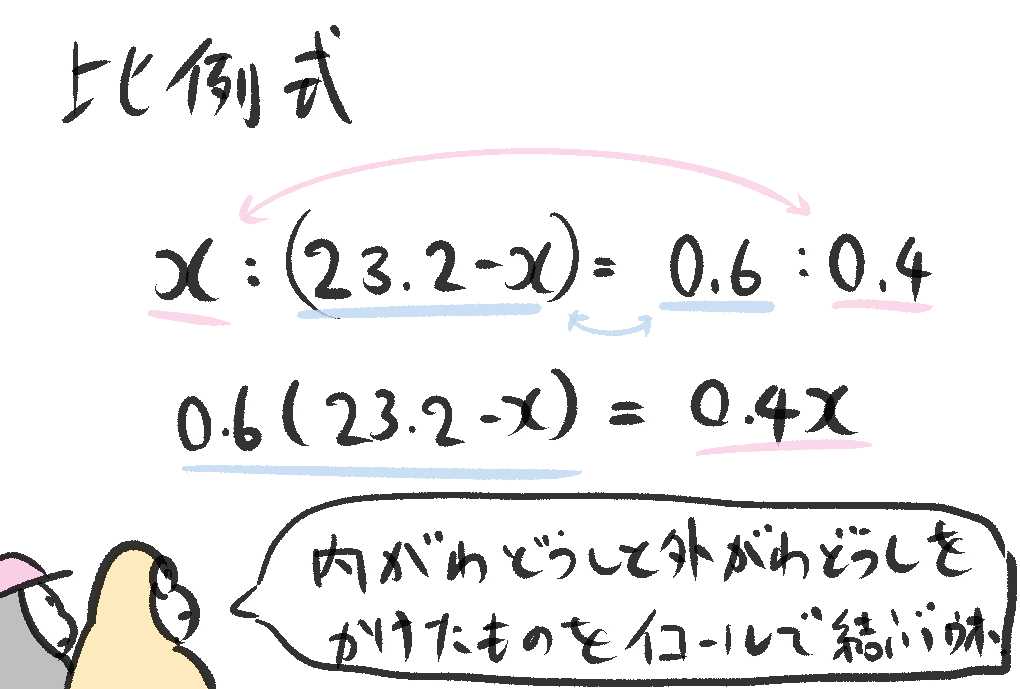
それをやると次の式が得られるウホ。

$(23.2 - x) × 0.6 = x × 0.4$

これをけいさんしていくと、$x = 13.9$になるから、食べられるバナナの長さはそれぞれ次のようになるウホ。

兄弟	長さ cm
兄	9.3
弟	13.9

比例式をつかわなくても、先に弟のぶんのながさ（23.2 * 0.6 = 13.9）を計算してから、全体からその長さをひいても同じウホ！やりやすいほうほうを選ぶといいウホ。

---

こたえ：

兄弟	長さ cm
兄	9.3
弟	13.9

---

きちんと割合を計算することができたウホ。でも、小数点以下までだしたものの、それをはかる定規📐がなかったから、けっきょくざっくりとわけあっていたウホ。

それもまたいいウホ！ときとばあいによっては、そういうおおざっぱな見積りも効果をはっきすることがあるウホ。けっきょく２人はまんぞくして帰っていったし、ゴリはきょうだいあいのほかにも良いことを学んだ気がするウホ。意気揚々とおうちに帰ることにするウホ。