ゴリラと学ぶ「俵杉算」ピラミッド編

いぜんにゴリラピラミッドのたかさをはかったお話をしたウホ。このゴリラピラミッドは、ゴリラ🦍がなんにんもつみかさなることでできているウホ。
ときどき、ゴリラたちはしょうどうてきにゴリラピラミッドをつくっていたりするウホ。ゴリもさんかしようとはおもっているけど、気が付いたらいつのまにかつくられているウホ。
ところで、ゴリはこのゴリラピラミッドに、どれくらいのゴリラ🦍がいるのかきになったウホ。たくさんいるといえばそれまでだけど、せっかくだしせいかくに数えてみたいウホ!
というわけで、ゴリラピラミッドをつくっているゴリラの数をかぞえるほうほうをかんがえてみるウホ。
もんだい
なんにんかのゴリラ🦍でできているゴリラピラミッドがあるウホ。
このゴリラピラミッドは、一段ずつゴリラがならんで、そのうえにもう一段ずつゴリラがならんで・・・をくりかえしてつくられているウホ。
奥行きはゴリラひとり分しかない、ぺらっぺらのピラミッドウホ。
さらに、このゴリラピラミッドは、一段ずつあがるにつれて、一段のゴリラの数は一人ずつへっていくウホ。
たとえば、五段のゴリラピラミッドがある場合には、5, 4, 3, 2, 1人のゴリラが一段ずつ、全部で五段のゴリラピラミッドを作るウホ。
ここで、もしゴリラピラミッドの一番下が、63人のゴリラで出来ているときには、
ゴリラピラミッドをつくっているゴリラは、全部で何人になるウホ?
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍
こたえ
いっこずつかぞえていくと、きりがないウホ!まずは、五段の例からなにか法則性をみつけたいウホ。
たとえば、ゴリラピラミッドが五段の時には、ゴリラは何人いるウホ?数えていくと、5 + 4 + 3 + 2 + 1 = 15人になるウホ。 一番下のゴリラの人数は5人だから、だいたいその3ばいということになるウホ。
ほかのパターンも考えてみるウホ。例えば、ゴリラぴらみっどが7だんの時をかんがえるウホ。
七段の時は、7, 6, 5, 4, 3, 2, 1で、全部足すと28人になるウホ。
今度は、一番下のゴリラの数の4倍になったウホ。
さらに他のパターンで、9段のときをかんがえるウホ。この時は、45人になるウホ。
9 × 5 = 45だから、今度は一番下のゴリラの数の5倍になったウホ。
そうすると、なんとなくの法則性として、一番下のゴリラの数に、一番下のゴリラの数に1を足したものを÷2したものをかけると、全部のゴリラの数になりそうウホ!
ということで、これをつかうと、63人のゴリラでできているゴリラピラミッドには、
$63 × \frac{63+1}{2} = 63 × 32 = 2016$
になったウホ!2016年にこれをやれば、だいぶおめでたいかんじになったけど、もう遅いウホ。ともかくゴリラの人数は求められたウホ。
…
じつは、この計算は、日本のニンゲンが江戸時代に書いた「俵杉算」とおなじ考え方ウホ。
このけいさんでも、おなじような公式をつかうウホ。一番下のゴリラの数を🦍とすると、ゴリラは全部で
$\frac{🦍(🦍+1)}{2}$
になるウホ。なぜこうなるかというと、ゴリラピラミッドをコピーして、逆さにしてもとのゴリラピラミッドにくっつけたものをかんがえるウホ。
これは、底辺が🦍+1の平行四辺形になるから、平行四辺形の底辺(🦍+1)に高さ(ゴリラピラミッドの一番下のゴリラの数 = ゴリラピラミッドの高さ = 🦍)を書けて、それを1/2することで元のゴリラピラミッドをつくっているゴリラの数(=三角形の面積)になるウホ。
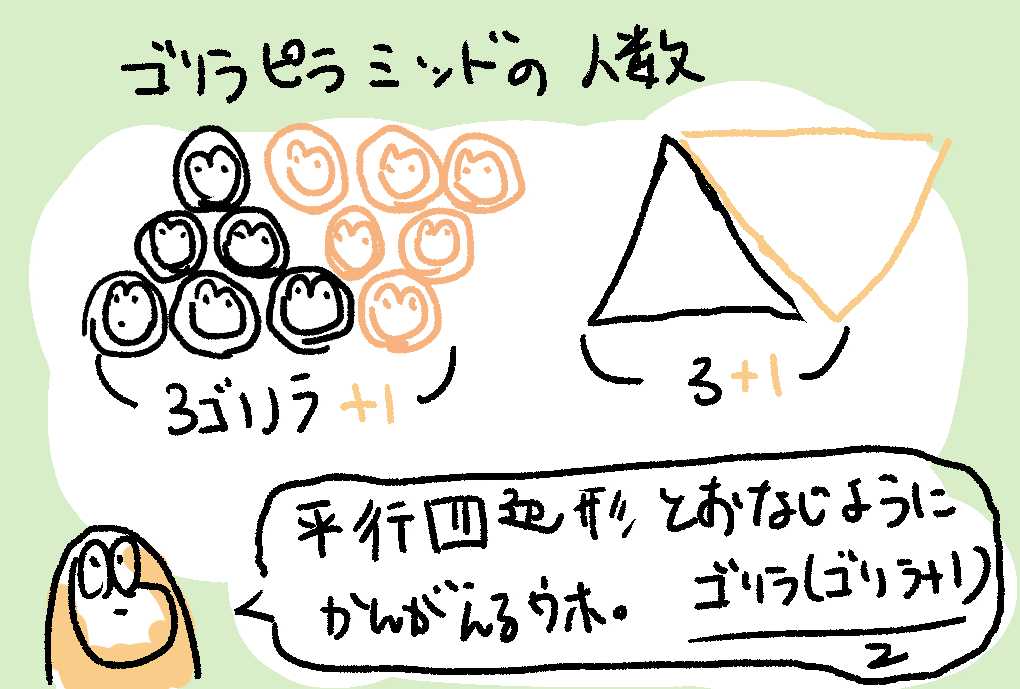
せんじんのちえはゆうこうにつかうに限るウホ!
こたえ:2016人
2016人もあつまってゴリラピラミッドをつくると、いちばんしたのゴリラがたいへんウホ。でも、ゴリたちゴリラたちは、くっきょうなからだをしているから、きっと大丈夫ウホ。そのうち、どれくらいの負荷がいちばんしたのゴリラにかかっているのかもけいさんしてみたいウホ。
あとは、ピラミッドが風にゆられるのも大変そうウホ。そのへんの風のえいきょうもそうちかんがえてみるウホ。