ゴリラと学ぶ「三平方の定理」地上の距離編

ゴリは高い木🌲にのぼったり、みわたす👀のがすきなのはまえにもいったとおり(三角比で木の上からゴリラのきょりをはかる)ウホ。
でも、ゴリの木🌲からどのくらいとおくまでみわたせるかは、たぶんかんがえたことがなかったとおもうウホ。
ナワバリをまもることを考えたら、みわたせるげんかいはかんがえたほうがいいかもしれないウホ。
こんかいは、木🌲のてっぺんとか、そういうたかいところからみわたせるきょり📏についてかんがえてみるウホ。
もんだい
ゴリが木🌲のうえからあたりをみわたしている👀ウホ。
あたりははればれとして🌞、すっきりととおくまでみえるウホ。
まわりには、じゃまになるようなほかの木はなくて、へいたんなじめんがつづいているとするウホ。
このとき、つぎのもんだいをかんがえてみてほしいウホ。
- 10 mの木のてっぺんからみえる範囲は、じめんのうえの距離でなんkmくらいになるウホ?
- 100 kmさきからみえるには、木のてっぺんまでの高さはどれくらいひつようウホ?
なお、地球の半径(せいかくには地球楕円体の長半径)は、赤道直下で6378.137kmとするウホ。
(さんこう:Wikipedia - 地球楕円体(最終更新 2019年3月8日 (金) 22:01))
海水面とか考えるのはめんどうだから、木は地球に直にせっしているとかんがえるウホ。
そして、ゴリたちは赤道直下にいるとかていするウホ。
🦍📏🦍📏🦍📏🦍📏🦍📏🦍📏
こたえ
ニンゲンがちゅうがっこうでならう、三平方の定理(ピタゴラスの定理)をつかうウホ!
三平方の定理は、まえに三角比で木の上からゴリラのきょりをはかるときにも触れたウホ。
…
- 10 mの木のてっぺんからみえる範囲は、じめんのうえの距離でなんkmくらいになるウホ?
まずは、地球上で、ゴリの木🌲(10 m = 0.010 km)と地球の半径(6378.137km)とのかんけいをかんがえるウホ。
ゴリは、地球🌍のうえにたっているから、いいかえると円にせっしていることになるウホ。
これもニンゲンが中学校でならったことで、円にせっしている線は、円の中心と垂直(せっしている線と半径とが90°のかんけい)になるってやつがあったウホ。
だから、地球の中心からゴリの木🌲のてっぺんまでの距離は、(6378.137 + 0.010) kmになるウホ。
木の上からみえる目線の先で、みきれるぎりぎりのところ(じめんかみずかわかんないけど、地平線とするウホ)は、これも地球とせっしているといえるウホ。
だから、地球の中心から地平線にある点までのきょりは、6378.137 kmになるウホ。
そして、ゴリの目線と地球とは、せっしているから、垂直なかんけいになるウホ。これで、(地球の中心 - ゴリの目線 - 地平線の点)で、直角三角形ができることになったウホ!
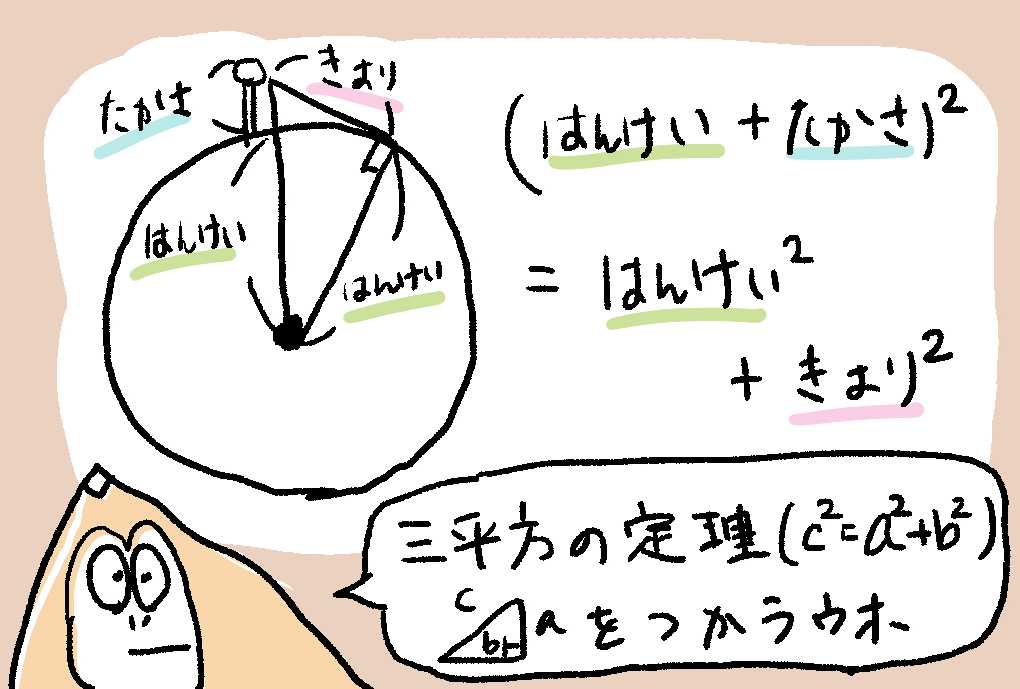
あとは、ゴリの目線から地平線の点までの距離を$x$として、三平方の定理をつかうウホ。
三平方の定理、$c^2 = a^2 + b^2$($c$が斜辺、$a, b$はほかの辺)をつかうと、つぎのようにかけるウホ。
$地球の中心からゴリの目線まで^2 = 地球の半径から地平線の点^2 + ゴリの目線から地平線の点^2$
ここから、
$(6378.137 + 0.010)^2 = 6378.137^2 + x^2$
で、$x$を計算すると、11.294 kmになったウホ!
ここで、もんだいでは「じめんのうえの距離でなんkm」か聞いていたウホ。
だから、ゴリの木がまっすぐ立っているとして、(木の根元 - てっぺん - 地平線の点)が、直角三角形になっていると考えるウホ。
そして、おなじように三平方の定理で、「木の根元から地平線の点までの距離」をけいさんするウホ。
かくのがめんどうだから、しょうしゃくすると、小数点第4位以下は四捨五入して、11.294 kmになるウホ!
四捨五入したら、目線から地平線の点までのきょりとおなじになったウホ。
…
- 100 kmさきからみえるには、木のてっぺんまでの高さはどれくらいひつようウホ?
計算をかんたんにできるように、さっきのもんだいから公式をつくってみるウホ。
地平線の点から木の根元までの距離を$x$、木の高さを$y$、地球の半径を$R$とすると、
$y = \frac{x^2}{2R}$
となるウホ1。
ここで、さっきの計算で、ざっくりだけど「地平線の点から木のてっぺんまでの距離」 = $x$とおくことができるとするウホ。 これをつかってけいさんすると、
$y = \frac{50.000}{2 × 6378.137}$
で、0.783 km = 783 mになるウホ!
こたえ:
- 11.294 km
- 783 m (0.783 km)
おかげでゴリがもっている木🌲からみわたせるナワバリ👀がわかったウホ!ゴリのナワバリがちょうど11.294 kmさきまでつづいていたら、ちへいせんの先からゴリラ🦍やニンゲン👫がみえたら、もういろいろいたずら👿しちゃうウホ。
2問目は、783 mもあると、もはや近代的なゴリラタワー🦍ウホ。そんなタワーをいつか立ててみたいウホ。
あと、とおくのものをみるとかすんでみえるのは、みんなもしってのとおりウホ。光💡と空気とのさんらんがかんけいしているとおもうんだけど、こんどやるときは、そんな減衰率?てきなのもかんがえてみたい👊ウホ。
さらに、天気⛅とのかんけいもけいさんできたら、ハッピー😊ウホ。
まず、木の根元までの距離$x$と、木の高さ$y$をつかうと、三平方の定理から、
$地平線の点から木のてっぺんまでの距離 = \sqrt{x^2 + y^2}$
になるウホ。
つぎに、(地球の中心 - 木のてっぺん - 地平線上の点)で直角三角形をつくったときは、
三平方の定理から、
$(R + y)^2 = R^2 + (\sqrt(x^2 + y^2))^2$
になるウホ。
これを展開すると、
$R^2 + 2Ry + y^2 = R^2 + x^2 + y^2$
になるウホ。
で、しきをせいりすると、うえにしめした公式になるウホ。
-
いちおうくわしくかいておくウホ。
地平線の点から木の根元までの距離を$x$、木の高さを$y$、地球の半径を$R$とするウホ。 ↩︎