ゴリラと学ぶ「三角比」木の高さ編

ゴリは高い木🌲にのぼるのが好き😍ウホ。高いところからみわたすと、いろいろなものがみえる👀ウホ。
ふと下をみてみると、ゴリラ🦍たちがちかづいてきていたウホ。
ゴリはいっこうにかまわないけど、なわばりをしらずに近づくと、ときにあぶない⚠目にあってしまうウホ。

こんかいは、木の上からもくてきのもののきょり📏をはかってみるウホ。

もんだい

ゴリが木🌲の上からみはっている🔭と、2人のゴリラ🦍が木にちかづいていたウホ。
木のうえからは、ゴリラ🦍たちへの木からのきょり📏はわからないウホ。
でも、角度📐はわかっているものとするウホ。

ゴリにわかることは以下のとおりウホ。

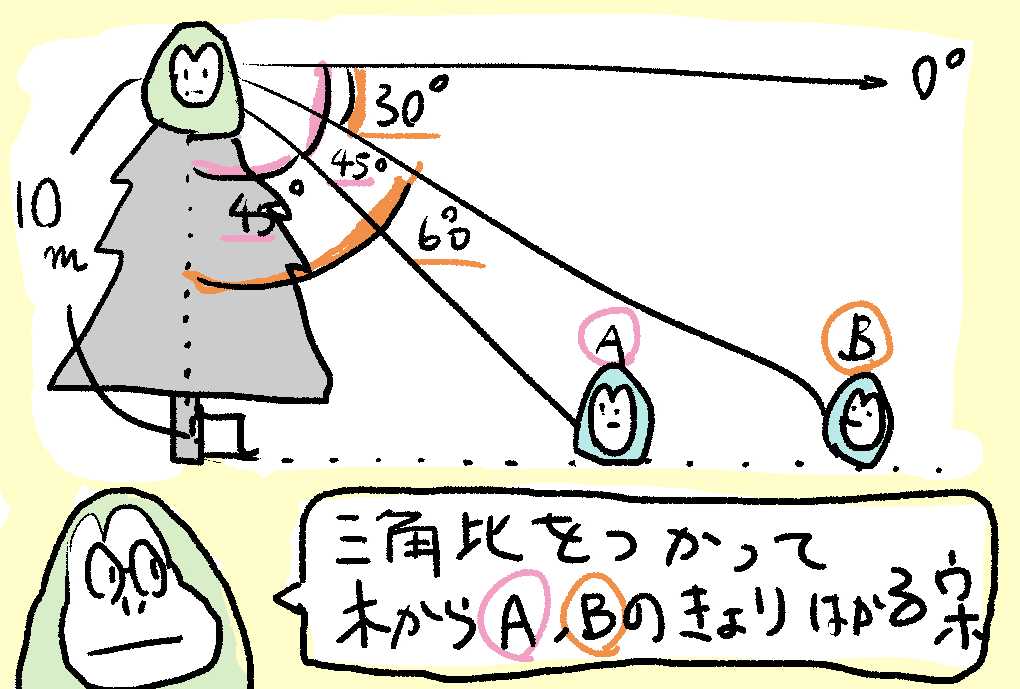
• ゴリのいう「角度」は、ゴリがまっすぐみた🔭ときを0°として、そこからみおろした角度📐をいうウホ。
• ゴリのいちから、ゴリラAへの角度📐は30°ウホ。
• ゴリのいちから、ゴリラBへの角度📐は45°ウホ。
• ゴリの目線から木のねもとまでは、ちょうど10 mとするウホ。

ゴリからみて、ゴリラAとゴリラBとのきょりは、それぞれどれくらいウホ？

ひつようなら、つぎのあたいを使ってもいいウホ。

なまえ	すうち（だいたい）
$sin45°$	$0.70$
$cos45°$	$0.70$
$tan45°$	$1.00$
$sin60°$	$0.87$
$cos60°$	$0.70$
$tan60°$	$1.73$

🦍🌲🌲🌲🌲🌲🌲🌲🌲🦍🦍

---

こたえ

①三角比をつかうほうほう

三角比をつかうウホ！こんかいのばあいは、ゴリがまっすぐみたところを0°としているウホ。
ちょっとややこしいけど、ゴリの目線と、木🌲とはすいちょくなかんけいウホ。
つまり、90°のかんけいにあるから、そこからうえにかいた「角度📐」をひいたら話がはやいウホ。

そうすると、ゴリラAとゴリラBとのつくる三角形📐はつぎの図のようになるウホ。

ここから、三角比できょりをけいさんするウホ。

三角形のたかさ（木🌲）は10 mだとわかっているから、木のたかさに三角比をかければいいウホ。
そうすると、ゴリラたちとのきょりはそれぞれつぎのようになるウホ。

ゴリラ	けいさんしき	けっか（きょり）
ゴリラA	$10×tan45°$	10.0 m
ゴリラB	$10×tan60°$	17.3 m

$tan$つかわなくても、$sin$と$cos$をくふうすればとけなくもないウホ。
けっかさえあっていればいいウホ。

②さんかくひをつかわないほうほう

ニンゲンはちゅうがっこうで、三平方の定理をまなんだウホ。
そのときに、直角いがいのかくどが（45°, 45°）（30°, 60°）のとき、
（$1 : 1 : \sqrt{2}$）、（$1 : \sqrt{3}$ : 2）（じゅんばんはてきとう）があったとおもうウホ。
それをおもいだせば、三角比をならってなくても、とけなくもないウホ。
そのときは、$\sqrt{3} = 1.732…$もしっているととけるウホ。

---

こたえ：ゴリラAとのきょりは10 m、ゴリラAとのきょりは約17.3 m

---

ゴリラ🦍たちはゴリの木🌲にちかづいてきたけど、ゴリにきがつくとはなれていったウホ。
これいじょう近づかなくてよかったウホ。ゴリはいたずら👿が好きだから、これいじょうちかづいていたらねじねじチョコパン💩をなげていたところだったウホ。