ゴリラと学ぶ「組合せ」

ゴリたちゴリラは、ニンゲンも生物の授業だったり保健体育の授業でならったかもしれないけど、オスとメスという性別がわけられているウホ。ゴリラが単為生殖しないかぎりは、きほんてきにオスとメスが交配することで子ゴリラがたんじょうするウホ。そんなわけで、ゴリ達のようなオスゴリラにとっては、メスゴリラとうまいこといろいろやって、じぶんの子孫を作っていくことはたいへんじゅうようなかだいになるウホ。
ジャングルの中にはいろいろなゴリラがいるから、どういうゴリラたちがペアになるか、そのパターンを一つ一つ確認していく方法はめんどくさいウホ。というわけで、こんかいはゴリラの組み合わせについて数学的に考える練習をしてみるウホ。
もんだい
あるジャングルに、ゴリラ🦍がたくさんいるウホ。ゴリラのなかにはオスゴリラとメスゴリラで明確にわけられているゴリラたちがいるウホ。
いま、ジャングルのなかにオスゴリラが50人、メスゴリラが48人いるウホ。これだけおおいとゴリラの合コンをするのにも大変そうだから、グループに分けていきたいウホ。
そこで、オスゴリラから4人、メスゴリラから4人をえらんでグループを作る時に、そのようなグループは何通り作れるのか答えてほしいウホ。
🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍🦍
こたえ
ニンゲンが高校数学でならう、組合せのかんがえかたをつかうウホ!ほかにもやりかたはあるかもだけど、こんかいは手っ取り早くこの方法で行くウホ。
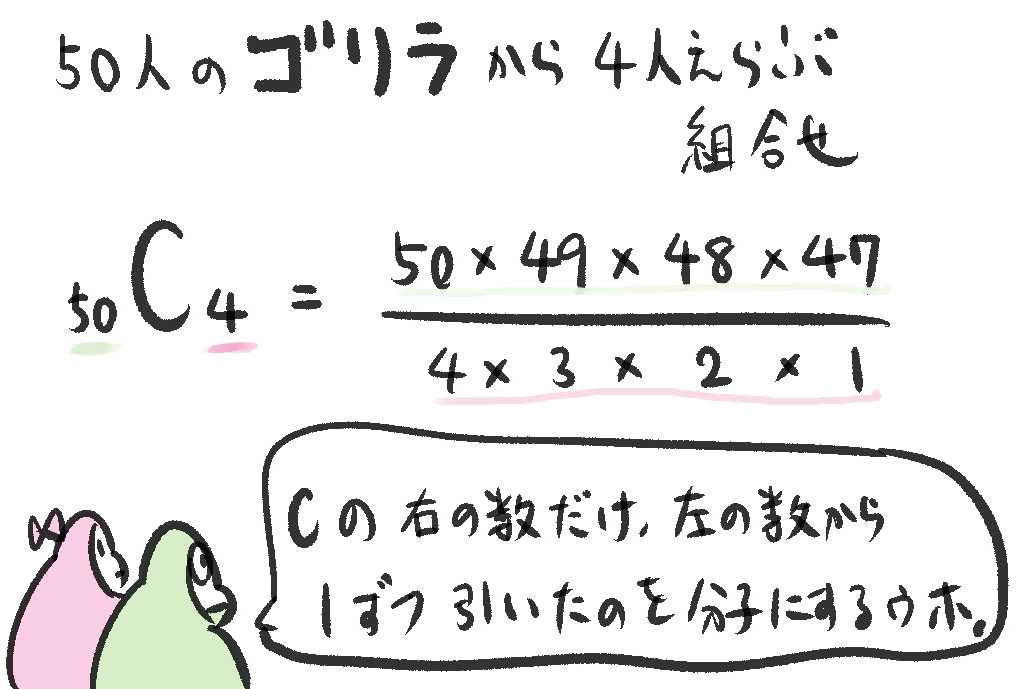
まず、オスゴリラ50人から4人をえらぶ方法は、組合せでいうと${}_{50}C_4$になるから、これは、
${}_{50}C_4 = \frac{50 × 49 × 48 × 47}{4 × 3 × 2 × 1} = 230300$
になるウホ。
つぎに、メスゴリラもおなじように計算すると、
${}_{48}C_4 = \frac{48 × 47 × 46 × 45}{4 × 3 × 2 × 1} = 194580$
で、あとはこれらを掛け算すると、
$230300 × 194580 = 44.8118 × 10^9$
で、だいたい45億通りになっちゃったウホ。とんでもない組合せの数ウホ!
こたえ: だいたい45億通り
ゴリラが100人くらい集まっただけでも、組合せがすごい数になっちゃったウホ!ここからさらに効率よくカップルの成立を目指すためには、きっと同じ性別の集団の中でもどのような配置をするのがその場の雰囲気的にバランスがいいのか、また違う性別にたいしてはどの異性同士のゴリラを対面させるとカップル成立の可能性が高くなるのか、いろいろ考えなくちゃいけない気がしてきたウホ!
こういうのがきっと、ちまたのニンゲンがつかっているマッチングアプリなんかにつかわれているかもしれないウホ。ゴリもそのうち、ゴリラのためのマッチング方法について考えてみたいウホ。